C语言中数字的存储方式
C 语言作为一种历史悠久的系统级编程语言,理解其底层数据如何存储是很有必要的。在它的基本数据类型中,有三类最为重要:「有符号数」,「无符号数」,「浮点数」,本文将分析这三种类型的数据在计算机内如何存储、表示、计算。
位、字节
不论是有符号数、无符号数还是浮点数,在机器内部都是以二进制来表示。在计算机内部,最小的数据单位是「位」,即一个0或1,目前通常由8位组成一个「字节」。这三种数据类型均由若干字节表示,也就是用「有限」数量的位来对数字进行编码,不同长度的位所能表示的大小也不同。
例如:short int 在64位机器上占2字节,当它存储有符号数2时,在小端法机器上其位级表示是:0000 0010 0000 0000。
大小端
在上面的 short int 例子中,我们提到了小端法,它与大端法是一对,用来描述数据的有效字节先后顺序 —— 最低有效字节在前的称为小端法,最高有效字节在前的称为大端法。仍以上面的 short int 为例,十进制 2 的二进制是 10,所以 2 在机器内的表示应该是 0000 0000 0000 0010,在小端法机器中,最低有效字节在前,所以应该是0000 0010在前,这就有了前面的结果。
实际上使用哪种字节顺序是任意的,目前主流的三大操作系统:Windows,macOS,Linux 都是小端法,在写程序时一般也无需关心机器到底是大端还是小端。
无符号数
无符号数指的是大于或等于0的整数,在 C 语言中定义无符号数的方法就是在 int,long,short,char 的前面加上 unsigned,随着数据类型的不同,其对应的无符号数所能表示的范围也不同。在 64 位机器上,典型的无符号数取值范围是:
| 数据类型 | 最小值 | 最大值 |
|---|---|---|
| unsigned char | 0 | 255 |
| unsigned short | 0 | 65535 |
| unsigned int | 0 | 4294967295 |
这个范围是如何得出的呢?这与无符号数的编码方式有关。因为它总是大于或等于0,所以不需要符号位,也就可以把它所占的字节都用来表示数据,就像单纯的使用二进制一样。如果以函数 B2U 来表示 w 位无符号数的位向量
\[\vec{x}\ \ \dot=\ \ [x_{w-1},\ x_{w-2},\ x_{w-3},\ \ldots,\ x_0]\]就是:
\[B2U_w(\vec{x})\ \ \dot=\ \ \sum_{i=0}^{w-1} x_i2^i\]例如:对于unsigned char类型来说,当位全为1时处于最大值,即: \[[1, 1, 1,1,1,1,1,1]\]
使用 B2U 来将其转换为无符号数就是: \[1 \times 2^7+1 \times2^6+1 \times 2^5+ \ldots +1 \times 2^1+1 \times 2^0 = 255\]
通过公式 B2U 可以看出,每一个位向量即01序列都唯一对应一个无符号数,反之亦然,所以无符号数可在取值范围内被精确表示。
有符号数
有符号数指的是值可能为负的数,在 C 语言中默认使用有符号数,不同于无符号数,有符号数不需要显式声明signed。与无符号数相同的是,不同的有符号数类型所能表示的范围也不同。在64位机器上,典型的有符号数取值范围是:
| 数据类型 | 最小值 | 最大值 |
|---|---|---|
| char | -128 | 127 |
| short | -32768 | 32767 |
| int | -2147483648 | 2147483647 |
可以看到原先无符号数的表示范围被一分为二,这是因为有符号数的最高位变成了符号位,该位表示值的正负情况,0表示正,1表示负,其余各位与无符号数的规则类似。如果仍以上面的位向量 \(\vec{x}\) 为例,以函数 B2T 来表示该位向量就是:
\[B2T_w(\vec{x})\ \ \dot=\ \ -x_{w-1}2^{w-1} + \sum_{i=0}^{w-2}x_i2^i\] 其中, \(-x_{w-1}2^{w-1}\) 就是最高位的符号位。
以 char 类型的位向量
\([1,1,1,1,1,1,1,1]\)
为例,使用 B2T 将其转换为有符号数就是:$$-1 \times 2^7 +1 \times 2^6 + 1 \times 2^5 + \ldots + 1 \times 2^0 = -1$$
在有符号数中,符号位的权重是 \(-2^{w-1}\) ,在 B2T 的计算过程中,只要符号位为1,则负权值为计算过程中唯一的负值,第 \(w-2\) 至 \(0\) 位中只要有某一位的值是1,都会使总体结果不断的趋向 \(-1\) ,如果全为1,经过计算则得到了最大的负数 \(-1\) ,要想得到最小的负数,只要只保持符号位为1,其他位不出现正数即可,即符号位为1,其他位全0: \([1, 0, 0, 0, 0, 0, 0, 0]\) ,这就得到了最小负数-128。
由此可以看出,有符号数的范围是不对称的,例如 char 的最小值 -128 并没有对应的最大值 128,其最大值是127,位级表示是 \([0, 1, 1, 1, 1, 1, 1, 1]\) ,如果对其 +1,位级表示变成了 \([1, 0, 0, 0, 0, 0, 0, 0]\) 。注意,这在位级表示上是正确的,但以有符号数的规则进行解释时,该值就变成了 -128,使用 C 语言验证确实如此。
有符号数与无符号数之间的转换
C 语言允许不同的数字数据类型之间做「强制类型转换」,不同类型的数据在运算中也会发生「隐式类型转换」,而这些类型转换往往是导致错误的原因,所以我们要了解类型转换的规则。数据类型转换的情况是多样的,例如 short 转换为 int,unsigned int 转换为 int,在本节中只讨论有符号数与无符号数的转换,也就是同样字长的 unsigned 与 signed 的相互转换。
从前文可以看到,有符号数与无符号数的在位级上的差别就是最高位是否为符号位,所以核心的一点就是有符号数与无符号数之间不论怎么转换,其「位模式」是不变的,也就是说该值的01序列不变,变的只是解释该序列的方法。
我们写一个简单的 C 程序来验证这一点:
1int main() {
2 signed char a = -12;
3 unsigned char b = (unsigned char) a;
4
5 printf("%d, %d", a, b); // -12, 244
6
7 return 0;
8}
在本例中 a 的位模式是 0xf4,当强制类型转换为 b 后,b 的位模式仍是 0xf4,这就说明了强制类型转换不改变位模式,只改变了解释位的方式。如果要手动计算 b 的结果,我们可以通过 B2T 反推出 a 的位模式,再通过 B2U 计算出该位模式对应的无符号数,而更方便的方法是通过这两个同时来推出一个新公式T2U。
如果我们计算 B2U 与 B2T 之差可以发现,从 0 到 w-2 位将相互抵消,只剩下一个 \(x_{w-1}2^w\) ,即
\[B2U_w(\vec{x}) - B2T_w(\vec{x}) = x_{w-1}2^{w-1} - -x_{w-1}2^{w-1} = x_{w-1}2^w\] 也就是说 \[B2U_w(\vec{x}) = B2T_w(\vec{x}) + x_{w-1}2^w\] 因为有无符号数的位模式不变,所以可以说二进制到无符号数等于二进制到有符号数加 \(x_{w-1}2^w\) ,而有符号数的位模式中 \(w-1\) 位决定了该数的正负,所以公式 T2U 可以归纳为:
\[T2U_w(x) = \begin{cases}x+2^w,\ \ x<0 \\\\x,\ \ \ \ \ \ \ \ \ \ \ x \geqslant 0\end{cases}\]例如上面的 C 程序中,a 的值为 -12,小于0,则其对应的无符号数为 -12 + 2^8 = 244。
根据上面 \(B2U_w(\vec{x})\) 与 \(B2T_w(\vec{x})\) 的关系,也可以说二进制到有符号数等于二进制到无符号数减 \(x_{w-1}2^w\) ,而无符号数的位模式中 \(w-1\) 位决定该数是否大于或等于 \(2^{w-1}\) ,所以公式 U2T 可以归纳为:
\[U2T_w(x) = \begin{cases} x\ \ \ \ \ \ \ \ \ ,\ \ x < 2^{w-1} \\\\ x - 2^w,\ \ x \geqslant 2^{w-1} \end{cases}\]下面写一个简单的 C 语言程序来验证:
1int main() {
2 unsigned char a = 229;
3 signed char b = (signed char) a;
4
5 printf("%d, %d", a, b); // 229, -27
6
7 return 0;
8}
此时变量 a 的值为 \(229\ >\ 2^7\) ,所以其对应的有符号数为 \(229 - 2^8 = -27\) 。
有符号数与无符号数的扩展与截断
上节说到同一字长有符号数与无符号数之间的转换,这节来讨论同一符号情况下数据的扩展与截断,简单来说就是 short 转换为 int,或 unsigned int 转换为 unsigned short。
将一个无符号数转换为一个更大的数据类型,只要在开头添加0,这称之为零扩展。将一个有符号数转换为一个更大的数据类型,因为最高位是符号位的原因,所以要在开头添加最高有效位的值,这称之为符号扩展。
例如
\[\vec{x} = [x_{w-1}, x_{w-2}, x_{w-3}, \ldots , x_0]\],如果 \(\vec{x}\) 为 unsigned char,则扩展至 unsigned short 后位模式为
\[[0, 0, 0, 0, 0, 0, 0, 0, x_{w-1}, x_{w-2}, x_{w-3}, \ldots , x_0]\]如果 \(\vec{x}\) 为 signed char,则扩展至 signed short 后位模式为
\[[x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-1}, x_{w-2}, x_{w-3}, \ldots , x_0]\]下面写一个简单的 C 语言程序来验证:
1typedef unsigned char * byte_pointer;
2
3void show_bytes(byte_pointer start, int len){
4 for (int i = 0; i < len; ++i) {
5 printf("%.2x ", start[i]);
6 }
7 printf("\n");
8}
9
10int main() {
11
12 unsigned char a = 123;
13 unsigned short b = a;
14
15 signed char c = -123;
16 signed short d = c;
17
18 show_bytes((byte_pointer) &a, sizeof(a)); // 7b
19 show_bytes((byte_pointer) &b, sizeof(b)); // 7b 00
20 show_bytes((byte_pointer) &c, sizeof(c)); // 85
21 show_bytes((byte_pointer) &d, sizeof(d)); // 85 ff
22
23 return 0;
24}
说完了数据的扩展,下面来看看数据的截断。数据的截断就没有扩展那么麻烦了,假设截断前的数据类型长为 w 位,截断至一个新的数据类型长度为 k 位,则只需丢掉原始数据类型的高 w-k 位即可,并且不论有无符号,都使用该规则。
下面写一个简单的 C 语言程序来验证:
1int main() {
2
3 unsigned short a = 12345;
4 unsigned char b = (unsigned char) a;
5
6 signed short c = -12345;
7 signed char d = (signed char) c;
8
9 show_bytes((byte_pointer) &a, sizeof(a)); // 39 30
10 show_bytes((byte_pointer) &b, sizeof(b)); // 39
11 show_bytes((byte_pointer) &c, sizeof(c)); // c7 cf
12 show_bytes((byte_pointer) &d, sizeof(d)); // c7
13
14 printf("%d\n%d", b, d); // 57 -57
15
16 return 0;
17}
从例子中可以看到,当无符号的 short 转换为 char 时,丢掉高字节(测试机器为小端法)30,低字节值为 0x39,即 57;当有符号 short 转换为 char 时,丢掉高字节 cf,低字节值为 0xc7,即 -57。
浮点数
前面的有符号数无符号数均只能表示整数,而浮点数可以用来表示小数,目前绝大多数编程语言都使用 IEEE-754 浮点数标准,通过理解该标准如何表示小数,我们可以解释以前在开发中的一些奇怪现象。
常见的浮点数格式有 32位的单精度 与 64位的双精度,IEEE浮点标准用 \(V = (-1)^s \times M \times 2^E \) 来表示一个数,其类似于科学计数法 \(EXP = a \times 10^n\) 。
在公式中各个部分的意义如下:
- s 表示符号位,用来决定这是正数(s=0)还是负数(s=1)。
- M 表示尾数。
- E 表示阶码,用来对浮点数加权。
对应于公式中的三部分,浮点数对位进行划分,来分别对这些值进行编码:
- 单独的符号位 s 直接编码。
- k 位的阶码字段 \(exp = e_{k-1} \cdots e_1 e_0\) 编码阶码 E。
- n 位小数字段 \(frac = f_{n-1} \cdots f_1 f_0\) 编码尾数 M,但编码出的值也依赖于阶码字段是否为 0。
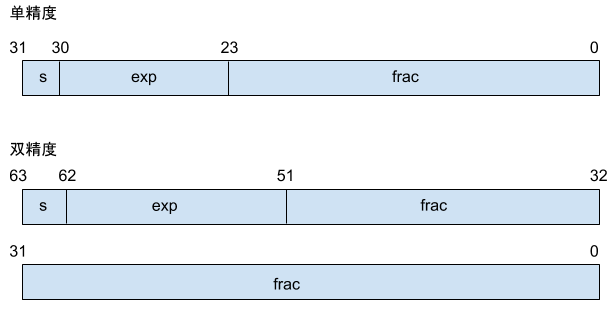
给定了位模式,根据 exp 的不同,被编码值可分为三种情况,下图以单精度为例:

1. 规格化的值
在最普遍的情况下,exp 的位模式不全为0,也不全为1(十进制的255),frac 任意,此时说该浮点数是一个规格化的值,其中阶码字段被解释为以偏置形式表示的有符号整数,即 \(E = e - Bias\) ,其中 e 即为 exp, \(Bias = 2^{k-1} -1\) 。
小数字段 frac 解释为描述小数值 f( \(0 \leqslant f < 1\) ),其二进制表示为 \(0.f_{n-1} \cdots f_1 f_0\) ,也就是说二进制小数点在最高位的右边。尾数定义为 \(M = 1 + f\) ,这称为隐含的以1开头的表示,这么做的原因是可以获得一个额外的精度位,即 \(M = 1.f_{n-1} \cdots f_1 f_0\)
2. 非规格化的值
当阶码全为 0 时,该浮点数是一个非规格化的值,此时阶码为 \(E = 1 - Bias\) ,尾数值为 \(M = f\) ,不包含开头隐含的 1。
非规格化有两个作用:首先,它可以来表示0。因为规格化数的尾数是隐含的以1开头,所以 \(M \geqslant 1\) 。而非规格化值的尾数不包含隐含的1,所以它可以用来表示0。它的另一个用途是表示那些非常接近于0.0的数。
3. 特殊值
特殊值有两种:无穷大与 NaN。
当阶码全1,小数字段全0时表示无穷大,这出现在两个非常大的数相乘或者除以零时,用无穷表示该结果,此时 s 为 1 时表示 \(-\infty\) ,s 为 0 时表示 \(+\infty\) 。
当阶码全1,小数字段非0时表示 NaN,即 Not a Number,当一些计算结果不是实数或无穷时,以 NaN 表示。
讲了一大堆理论,现在来实际计算一下。简单起见,假设有基于 IEEE 浮点格式的 5 位浮点表示,有 1 个符号位,2 个阶码位,2 个小数位:
\([0\ 00\ 10]\)阶码为全0,这是一个非规格化数,所以
- \(E = 1 - Bias = 1 - (2^{k-1} - 1) = 1 - (2^{2-1} -1) = 0\)
- \(2^E = 2^0 = 1\)
- \(M = f = 0.f_{n-1} \cdots f_1 f_0 = 0.10 = 1 \times 2^{-1} + 0 \times 2^{-2} = \frac{1}{2} \)
- \(V = (-1)^s \times M \times 2^E = (-1)^0 \times \frac{1}{2} \times 2^0 = 0.5\)
阶码非全0非全1,这是一个规格化数,所以
- \(E = e - Bias = 2 - (2^{k-1} - 1) = 2 - (2^{2-1} -1) = 1\)
- \(2^E = 2^1 = 2\)
- \(M = 1.f_{n-1} \cdots f_1 f_0 = 1.10 = 1 \times 2^0 + 1 \times 2^{-1} + 0 \times 2^{-2} = \frac{3}{2}\)
- \(V = (-1)^s \times M \times 2^E = (-1)^1 \times \frac{3}{2} \times 2 = -3\)
如果看懂了上面两个例子,那么 IEEE 浮点数的编码方式可以说基本掌握了,下面来探讨一些细节问题。
刚开始看你可能会对 M 的计算过程感到疑惑: \(M = 1.f_{n-1} \cdots f_1 f_0\) 或 \(0.f_{n-1} \cdots f_1 f_0\) ,这个是如何计算成小数的呢?
以 \([1\ 10\ 10]\) 为例, \(M = 1.10\) ,这里的 M 是二进制小数。十进制小数的表示形式为:
\[ d_md_{m-1} \cdots d_1d_0\ .\ d_{-1}d_{-2} \cdots d_{-n} \]其中 \(d_i\) 的范围是0-9,即
\[d = \sum_{i=-n}^m 10^i \times d_i \]类似的,对于二进制小数
\[b = \sum_{i=-n}^m 2^i \times b_i \]所以
\[ M = 1.10 = 1 \times 2^0 + 1 \times 2^{-1} + 0 \times 2^{-2} = \frac{3}{2} = 1.5 \]又以 \([1\ 10\ 11]\) 为例,
\[ M = 1.11 = 1 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-2} = 1 + \frac{1}{2} + \frac{1}{4} = 1.75 \]在这里尾数仅加了1,所能表示的值就从1.5到了1.75,也就意味着1.5-1.75之间的值无法被精确表示,当然现在尾数仅2位,精确表示的能力比较弱,如果是32位浮点数或64位浮点数,尾数有23位或52位,那能精确表示的数就多了,尾数的位数越高,所能表示的值越多,所能表示的值的间距越小。但是即使是它们也无法精确表示每一个数,对应无法精确表示的值只能进行舍入。
下面写一个简单的 C 语言程序来看下 float 类型的数据是如何存储与表示的
1int main() {
2 float a = 1.25;
3 show_bytes((byte_pointer) &a, sizeof(a)); // 00 00 a0 3f
4 return 0;
5}
因为是小端法机器,所以真实的位级表示是
\[[0\ 01111111\ 01000000000000000000000]\]这显然是一个规格化数,所以:
- \(E = e - Bias = 127 - (2^{k-1} - 1) = 127 - (2^{8-1} - 1) = 0\)
- \(2^E = 2^0 = 1\)
- \(M = 1.f_{n-1} \cdots f_1 f_0 = 1.01\cdots0 = 1 \times 2^0 + 1 \times 2^{-2} = 1.25\)
- \(V = (-1)^s \times M \times 2^E = (-1)^0 \times 1.25 \times 1 = 1.25\)
计算结果1.25就是变量 a 的值。
总结
本文简要的概括了有符号数、无符号数、浮点数在机器内的表示与转换,并举了些简单的例子,以求能对这几种数据类型的工作方式有一个大概的了解。