加法器是如何工作的
大部分人应该都听过加法器这个东西，顾名思义就是用硬件电路实现两个数的加法。加法器是构成计算机的基础，现代计算机中的加法器与加法器最初诞生时候的样子已经大相径庭，但其核心原理还是基本相同的，都是通过「逻辑门」来进行运算。在学习加法器的知识之前，我觉得这太神奇了，咔咔通个电就把结果算出来了，但其实它的构成非常简单。
首先需要说明，这里的加法器指的是「二进制加法器」，就是只能用于二进制加法运算，因为数字电路通常以二进制为基础，所以二进制加法器也是最普遍的。
继电器
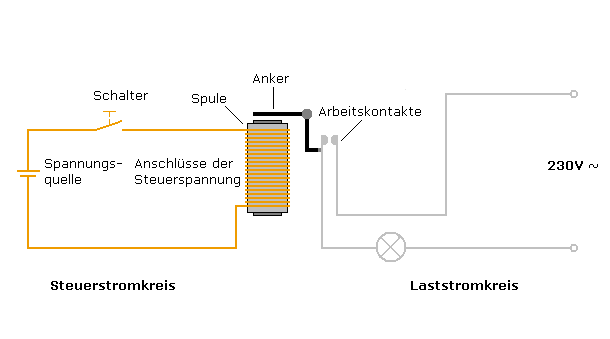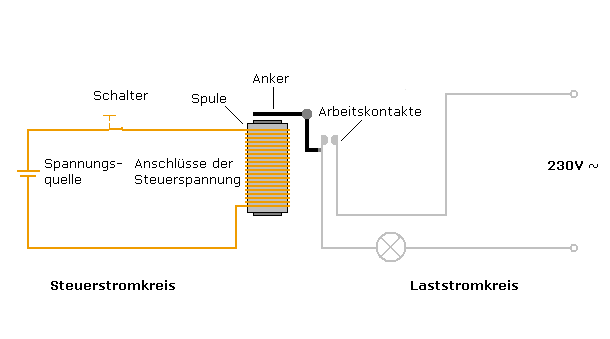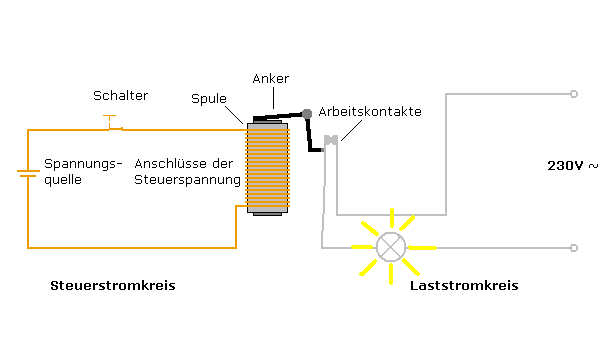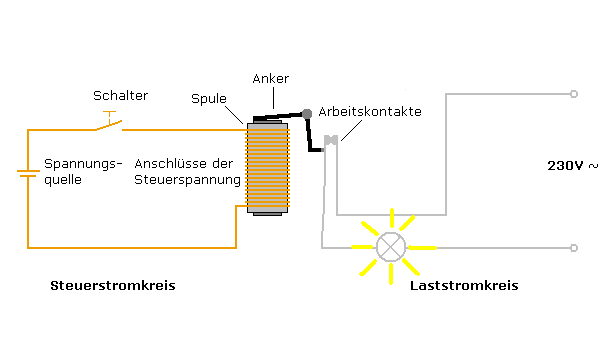
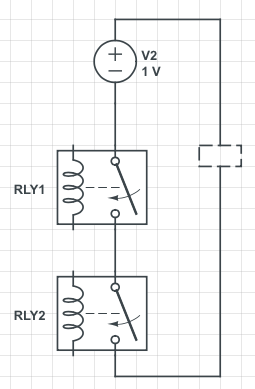
继电器是一种以电流驱动的机械控制元件，通过一个较小的电流来控制较大电流的开关。
(图片来源于wikipedia)
当左边的回路闭合，电磁铁产生磁力把Anker吸下来，Anker又造成了右边回路的闭合，就是这么简单。继电器是加法器必不可少的组成部分，不过随着科技的发展，加法器内不再使用继电器了，现在以晶体管来代替，但其基本原理还是相同的，本文以简单起见仍使用继电器来构成加法器。
逻辑门
接下来是最核心的部分：「逻辑门」。它的原理很简单，就是基于电路的通断。来看下下面的电路：
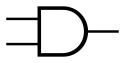
只有当A与B这两个继电器通电闭合后，右边的电路才形成回路，这时可以说只有当A与B同时闭合时，电路才形成回路。可能你会觉得这跟编程语言里的逻辑运算符&&作用一样啊，其实这确实是一回事，在20世纪30年代，香农提出了布尔表达式可以在电路中实现，他将布尔代数与电路联系了起来。继续回到这里，采用这种形式的电路，我们称其为「与门」，与门接收两个输入，只有当两个输入同时接收到信号时才会产生输出，如果用编程语言的概念来理解的话，就是只有A与B都为「true」，A && B才为true。与门的电气学符号与真值表如下所示：
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
如果你看懂了与门，那就应该能猜得到其他几种逻辑门是如何构造的了，他们的核心原理都是由继电器来控制整体回路的通断，在这里就不把每种逻辑门的详细构造画出来了，以下均以电气学符号代替，详细的构造可以查看wikipedia。逻辑门有多种，在加法器中只用到了三种：「与门」、「或门」、「异或门」。
异或门的符号为：
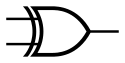(图片来源于wikipedia)
它的真值表为：
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
或门的符号为：
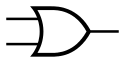(图片来源于wikipedia)
它的真值表为：
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
半加器
下面就开始来正式构造一个加法器了，首先来从算数角度来看下二进制的加法。二进制的加法表如下：
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
加上先导0的话则是：
| + | 0 | 1 |
|---|---|---|
| 0 | 00 | 01 |
| 1 | 01 | 10 |
下一步来从和与进位这两个维度来看，则可以得出下面两个表：
| 和 | 0 | 1 |
|---|---|---|
| 0 | 00 | 01 |
| 1 | 01 | 00 |
| 进位 | 0 | 1 |
|---|---|---|
| 0 | 00 | 00 |
| 1 | 00 | 01 |
这时你会神奇的发现，和与进位这两个表分别对应「异或门」与「与门」的真值表，这时二进制加法就与电路联系起来了，我们可以分别用一个异或门和与门来表示和与进位：
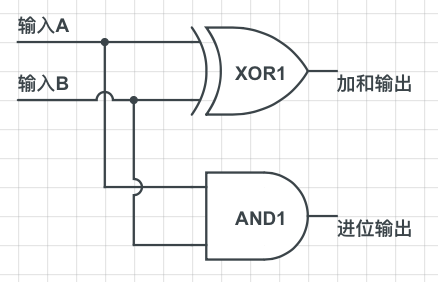
如上图所示，输入A和输入B分别为两个二进制数，当输入产生时，异或门将产生一个加和输出，与门产生一个进位输出，这就实现了上面加法表的规则，这种电路结构称为「半加器」。但它是不完美的，它不能处理两个多位二进制数加法产生的可能的进位，所以接下来就由「半加器」升级到「全加器」。
全加器
全加器的构造如下图所示：
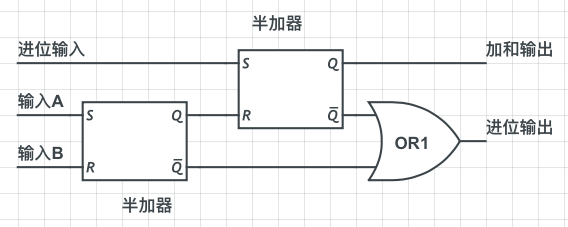
它由两个半加器和或门组成。进位输入接收上一位运算产生的进位输出（如果这是第一位则无输入），进位输入与输入AB产生的进位输出通过半加器产生一个总体的加和输出，同时他们的进位输出与输入AB产生的进位输出通过一个或门产生一个总体的进位输出，这样就运算完了。
以上构造的电路就称为「全加器」，它能完整的处理二进制加法中的加和与进位。不过此时的全加器依旧只能处理一位二进制数的加法，如果希望算一个多位的，则只需简单的将多个全加器连接起来即可：
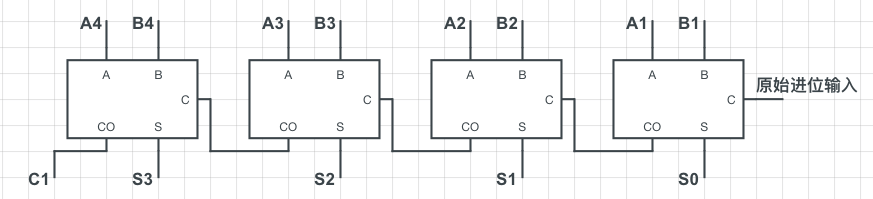
上图就是一个「4位全加器」，A1-A4，B1-B4分别表示两个二进制数的每一位输入，原始进位输入为0（低电平），S0-S3为每次的加和输出，因为4位加法有可能因为进位产生5位的结果，所以总的结果还要包含C1这个最后一个进位输出，到此，一个加法器就实现了，如果还想实现更高位数的二进制加法，只要依次再加几个全加器即可。